Bu yazım gerek örnekleri ile Rehber, gerekse matematiksel ifadeleri ile görüntü işlemenin mantalitesini kavramamızı sağlayacak bir kaynak kıvamında olsun istiyorum. Bu niyetlerle ilk satırlarıma başlıyorum ve sizleri oldukça uzun bir yazıya davet ediyorum…

Aslında böyle bir kaynak yazmayı baştan beri düşünüyordum. Bir süredir pek çok farklı konuda kullandığım için, OpenCV şu kadar önemli bu kadar önemli, efendim işte sektör, endüstri bla.. bla… demeyeceğim. Zaten zibilyon tane bu konuda kaynak var. Açıkça amacımı söyleyim: OpenCV ile alakalı birkaç bişey yazıyorsun yüzlerce gönderi etkileşimi geliyor. Bunun sebebi insanların arayışta olması.

İki çeşit insan var arayışta olan. İlki gerçekten öğrenmek isteyen insanlar, kendimi bu alanda uzman nasıl yapabilirim. İkinci çeşit ise şov yapmak için sourcehopper’lık yapanlar, bunlar çıkar yok yüz tanıma yapalım yok “3 adımda şundan yapalım ewle wele hebele hubele…” diye yazar durur. Bunlar her konuda her haltı bilirler ve parça parça kimden ne kod koparırsam diyen kişilerdir (ki onlarla uğraşmaktansa Github CoPilot kullanmak daha yararlı aslında, veya direk kodu ChatGPT’ye yazdır ne uğraşıyorsun tık derdindeki adamlarla)

Ben birinci çeşit insanı koparmak istiyorum. OpenCV Nedir yazımla bu yüzden başlamıştım ama devamı bu güne kısmetmiş.

İnsanlar öğrensin istiyorum veya öğrenmeye olan istekleri kafalarında şekil bulsun istiyorum. Şimdi bu serinin ki artık seri midir bilmiyorum 2. Yazısıyla (bikaç sene sonra :D ) devam ediyorum. Kod örnekleri de vererek OpenCV’de basit image manuplation işlemleri yapacağız şimdi. İyi okumalar.

Giriş

Neden bilgisayarlı görü diye yazmaya başlamadım da görüntü işleme ve ecnebilerin tabiri ile image processing dedim veya anlatacağım konulara doğru kaydırırsam image manuplation diyebilirim. Çünkü bu yazıda anlatacağım iş görü değil bu iş manuplasyon işi. Peki nedir bu image manipulation. Aslında burada yaptığımız, görüntülerin bilgisayar ortamında değiştirilmesi veya düzenlenmesi işlemidir. Bu işlemler arasında resimlerin boyutlarının değiştirilmesi, renklerinin düzenlenmesi, efektlerin eklenmesi, öğelerin eklenip çıkarılması gibi işlemler yer alır.

Bu işlemler dijital görüntüdeki pikseller üzerinde işlem yapmayı gerektirir. Peki piksel nedir? Neden dijital görüntü işleme diyoruz? Görüntü işlemenin matematiği nedir? Başladığımıza göre taaaa filmli makineler dönemine hatta ilk kameraya kadar geri dönelim.

İlk makineler “Camera Obscura” dönemlerini temel alıyor.

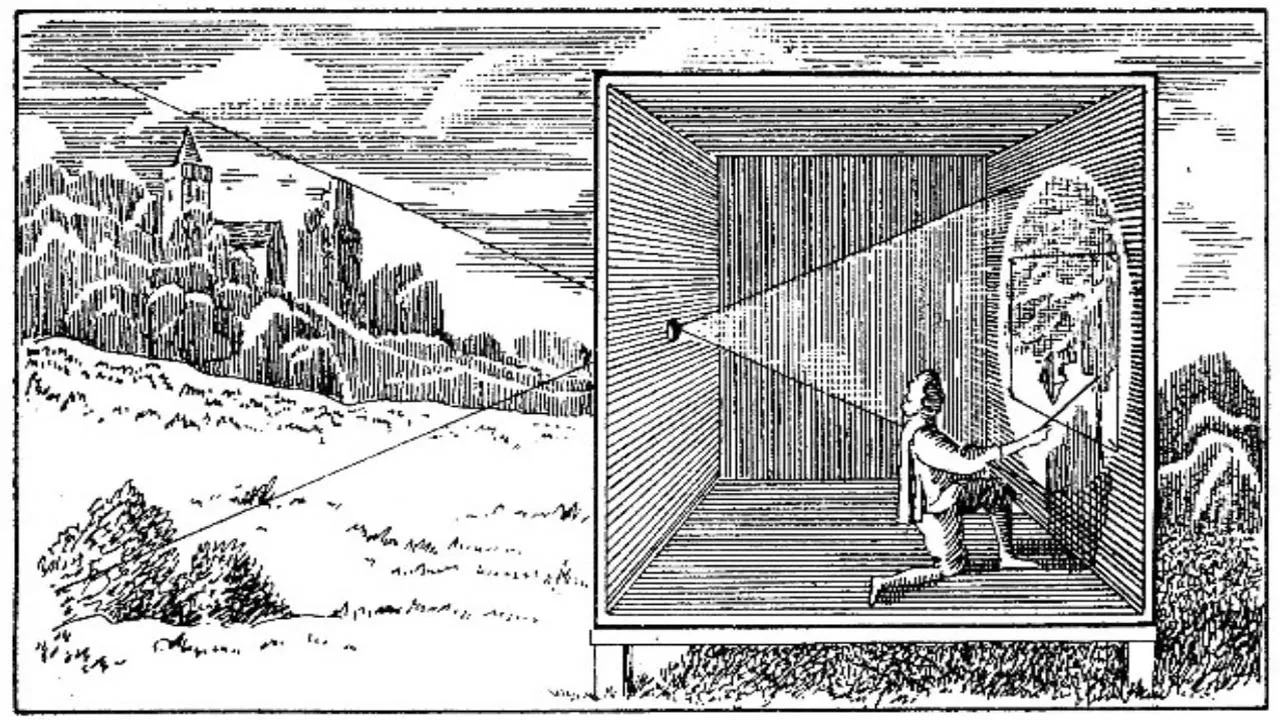
Camera Obscura basit bir ışık yayılımı mekaniğini anlamak için kullanılan bir yöntem sonucunda ortaya çıkmıştır. Yukarıda gördüğümüz gibi ufacık bir delikten geçen ışık perdeye ters olarak düşerek bir görüntü oluşturmakta. İlk kameralar da tam böyle bir diafram dediğimiz açıklık içinden geçen ışınların baş aşağı olarak bir noktaya düşürülmesi ve bu noktada bir şekilde o anın yakalanmasını hedefler.

Anın yakalanması demişken, bunun için şimdi bu fizik fenomenine birazcık kimya ekleyelim. Başrolümüz “gümüş nitrat”. Yine böyle ufacık bir delikten geçen ışığı kısa bir diyafram üzerindeki gümüş nitrat ve sodyum içeren ince bir filmin üzerine düşürüyoruz. Temelde bu teknik X-Ray filmlerindeki gibi bir teknik, X ışını kaynağı üzerimizden geçip filmin üzerine düştüğünde nasıl katı kısımlarımıza uğrayan X ışını soğurulduğu için filmin kemiklerimize gelen kısımları daha karanlık, diğer kısımlar daha aydınlık çıkıyorsa, bu film de üzerine düşen ışığın miktarına bağlı olarak daha aydınlık ve karanlık çıkıyor. Hatta pozlama konusu da tamamen filmin üzerine düşen ışıkla alakalı. Neyse o belki ileride analog fotoğrafçılığın hakkında yazarken (bir yazı yazarsam bu konuda) anlatacağım şeylerden birisi.

Filmler esasında negatif olarak çıkıyor makineden (ilerleyen başlıklarda lenna bacımızı negatifleyince buna ne gerek var dediğinizde bu bilgiyi unutmazsanız buna ne gerek var demezsiniz.)

Negatif fotoğraflarda orijinali mavi olan yerler sarı, yeşile duyarlı olan tabakada orijinali yeşil yerler megenta, kırmızıya duyarlı tabakada orijinali kırmızı yerler camgöbeği (cyan)olarak görünürdü ve film yıkama işleminin ardından bu negatif resim uygun şekilde işlenerek renkli kağıda basılırdı. Mavi sarıya, yeşil magentaya, kırmızı camgöbeğine… mavi, yeşil, kırmızı… sarı, magenta, camgöbeği… Doğru tahmin. Bugün modern fotoğrafçılıkta kullandığımız CMYK (Cyan-Magenta-Yellow Key, K harfi burada key dediğimiz kontrast tonudur) ve RGB renk şemaları tam da bu dönemden kalan bilgilerden dolayı böyle. Yani kimya fizikle bir oldu diyebiliriz.

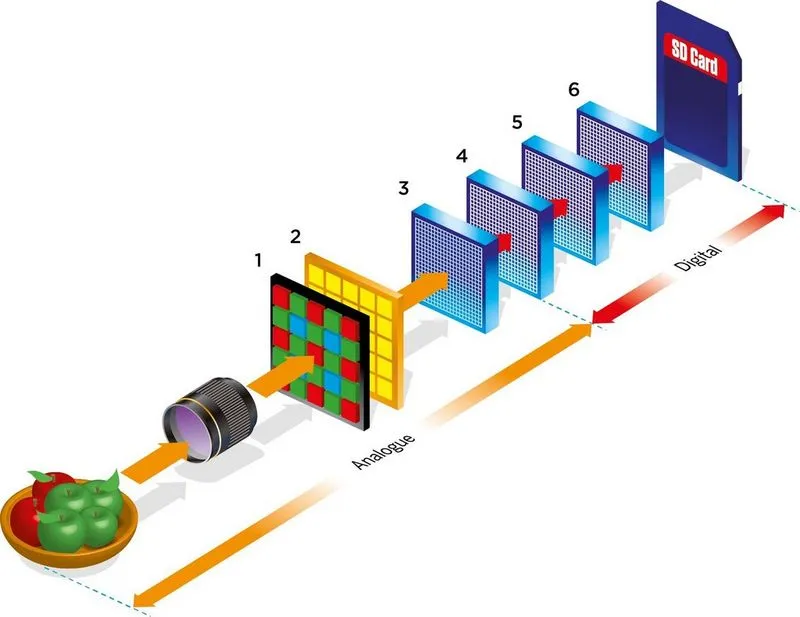
Modern kameralar ise tam manasıyla bu fiziği taklit eden güzel sensörlere sahip, artık ne biliyoruz, bir rengi elde etmek için CMYK veya RGB renklerine ihtiyacımız var. Eğer bu renklere ihtiyacımız varsa, sadece bu renklerin birisinin tonunu veren bir sensöre sahip olduğumuzda 3 sensör ile bir ışığın rengini belirlememiz mümkün. Nasıl ki analog makinelerde filmin üzerine düşen ışık onun üzerinde bir iz bırakıyorsa biz de diyotlar kullanarak üzerine düşen ışığın sinyal seviyesini ölçerek görüntüyü dijitalleştirebiliyoruz. Oldukça havalı…

Ve işte bu dijitalleşmiş görüntü üzerinde işlem uygulamaya da biz dijital görüntü işleme diyoruz.

Peki OpenCV Nereden Çıktı?

İşte bu dijital görüntülerin oluşturulmasından sonra İntel’in 1999 yılında Rusya’daki Moskova Merkezinde dijital görüntü işleme kütüphanesi olarak geliştirilmeye başlandı, 2000’de ise ilk alfa sürümü duyrulmuştur. Ama tarihle pek bir işimiz yok devam ediyorum şimdi görüntü işlemenin matematiği ile…

Dijital Görüntü İşlemenin Matematiği

OpenCV ile göbekten bağlı bir konuya değineceğim. Her pikselin ve her filtrenin ardında, zengin bir matematik dokusu yatar. Daha öncesinde söylediğim gibi renkleri RGB veya CMYK tonlarından her birisinin kombinasyonu olarak ifade edebiliriz. Olur da analog filme yakından bakacak olursak tam olarak göreceğimiz şey ışığa göre farklı oranlarda etkilenmiş ve tonlanmış bir kağıt olacak. Aynen bu aşağıdaki gibi.

Şimdi bu kağıdı bölebileceğimiz en ufak parçalara bölüp her bir parçayı işlemek için farklı bir nokta olarak alacak olursak bu noktalar bizim piksellerimiz oluyor. Bu pikseller RGB için her bir renk değerinin 0’dan 255’e kadar bir değer alır. Bir dijital görüntünün özünde, bu sayıların bir koleksiyonu yatar. Bir gri tonlamalı görüntüde, her piksel bir yoğunluk değeri ile temsil edilir; renkli bir görüntüde ise, her piksel genellikle kırmızı, yeşil ve mavi (RGB) kanallara karşılık gelen üç değerden oluşur.

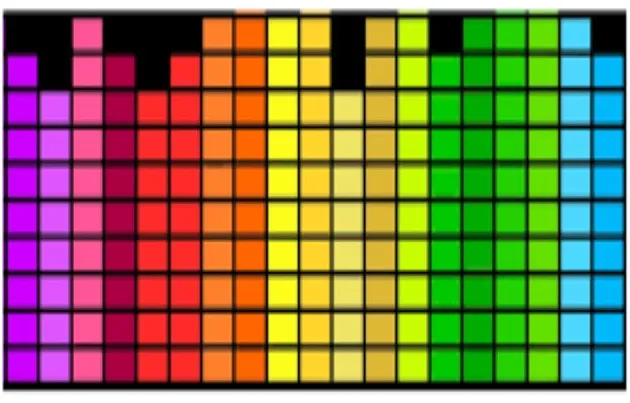
Böylece analog olan görüntü verisini dijitalize etmiş oluruz.

Matematiksel olarak, bir görüntüyü şu şekilde bir matris (ya da matrisler kümesi) olarak düşünebilirsiniz. M_x_N boyutunda bir fotoğraf için I değerini 3 değerli bir vektör olarak düşünecek olursanız.

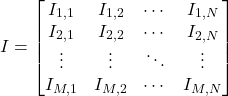
olarak ifade edebilirsiniz. Bu temsil, ilerleyen adımlardan göreceğimiz görüntü işleme teknikleri için görüntüler üzerinde çok çeşitli işlemleri gerçekleştirme amacıyla lineer cebirden yararlanmamıza olanak sağlar.

Ve OpenCV tam bu noktada işimize yarar. Kendisi bir kütüphane olarak dijital görüntü işlemede kullanılabilecek bütün lineer cebir tabanlı methodları son kullanıcı olan programcıya basitçe sunan bir araçtır. Bir nevi güzel bir çekiç.

Peki neden lineer cebire ihtiyaç duyuyoruz. Lineer cebir, matrisler ve vektörlerin dilidir ve birçok görüntü işleme tekniğinin temelini oluşturur. Lineer cebir sayesinde görüntü işlerken 3 temel yöntemi kullanırız.

• **Matris İşlemleri: **Toplama, çarpma ve transpozisyon gibi temel işlemler, görüntüler üzerinde küresel değişiklikler yapmamızı sağlar. Örneğin, bir dönüşüm matrisi uygulamak, görüntüyü döndürmeye, ölçeklendirmeye veya çarpıtmaya yarar.

• **Özdeğerler ve Özvektörler: **Bu kavramlar, görüntü sıkıştırma ve özellik çıkarımında kullanılan Temel Bileşen Analizi (PCA)gibi tekniklerin merkezinde yer alır.
• **Tekil Değer Ayrışması (SVD): **SVD, bir görüntü matrisini üç daha basit matrise ayırır ve görüntünün özsel özelliklerini ortaya çıkarır. Gürültü azaltma ve görüntü sıkıştırma gibi işlemlerde sıkça kullanılır.

Biraz Daha Matematik: Filtreleme ve Konvolüsyon

Filtreleme görüntü işleme ve iyikleştirmenin temel taşlarından birisidir. Görüntü işlemede filtrelemenin yapılmasını sağlayan en temel işlemlerden biri konvolüsyondur. Konvolüsyon, kernel veya filtre olarak bilinen küçük bir matrisin, görüntü üzerinde kaydırılarak piksel değerlerinin ağırlıklı toplamının hesaplanmasını içerir. Bu işlem yumuşatma (bulanıklaştırma) amacıyla, yani komşu piksel değerlerinin ortalamasını alarak gürültüyü azaltmak amacıyla; kenar tespiti, yani hızlı yoğunluk değişimi olan bölgeleri vurgulayarak kenarların belirginleşmek amacıyla kullanılabilir.

Matematiksel olarak f(x, y) ile ifade edeceğimiz görüntü matrisi ile h(x, y) olarak ifade edeceğimiz çekirdek matrisinin konvolüsyon işlemi şu şekilde tanımlanır:

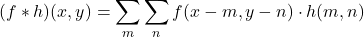
Bu işlemi okuyunca kafanızda belirmedi değil mi?

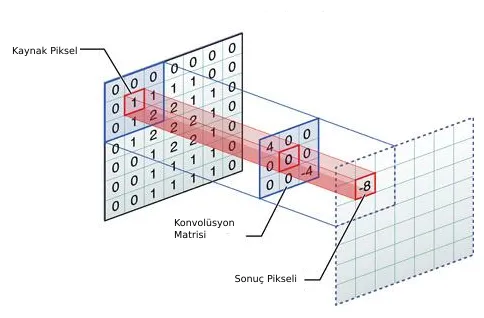
Peki şimdi :)

Bu basit fakat güçlü kavram, birçok filtreleme tekniğinin temelini oluşturur ve modern bilgisayarla görmede konvolüsyonel sinir ağları (CNN’ler) gibi daha ileri yöntemlerin temelini atar. Ama o bir başka yazımın konusu olacak

Ve Biraz Daha Matematik….

Aslında matematiğine girmişken biraz daha derin konulardan devam etmek mantıklı geldi. Özellikle görüntü işleme alanında matematiksel o kadar fazla methodoloji var ki. Bunlardan bazıları ile devam edeceğim:

Fourier Dönüşümü ile Frekans Alanı Analizi

Konvolüsyon ve diğer uzamsal işlemler görüntüleri piksel alanında işlerken, bazen görüntülerle frekans alanında çalışmak daha kolay olabilir. Frekans bileşenleri üzerinde yapılan değişikliklerle, gürültünün filtrelenmesi veya daha az önemli frekansların atılması yoluyla görüntü sıkıştırma gibi işlemler gerçekleştirilebilir.

İşte bu noktada Fourier Dönüşümü devreye girer. Fourier Dönüşümü, bir görüntüyü sinüs ve kosinüs bileşenlerine ayırarak, onu mekandan ziyade frekans cinsinden temsil eder. Burada iki farklı yöntem vardır kullanabileceğimiz.

• **Ayrık Fourier Dönüşümü (DFT): **Dijital bir görüntüde, DFT frekans içeriğini analiz etmek için kullanılır.

( M x N ) boyutlu bir görüntü için formülü şu şekildedir:

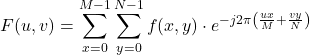
• **Hızlı Fourier Dönüşümü (FFT): **DFT’yi hesaplamak için verimli bir algoritma olup, gerçek zamanlı frekans alanı işlemlerini mümkün kılar. Hatta gerçek zamanlı sinyal işleme çalışanlar da kendisini yakından bilir.

Çok Ölçekli Bir Yaklaşım: Waveletler

Waveletler, özellikle bir görüntünün özelliklerini farklı ölçeklerde incelemek istediğinizde, analiz için alternatif bir yol sunar. Fourier Dönüşümü, sonsuza kadar uzayan sinüs ve kosinüs fonksiyonlarını kullanırken, waveletler hem uzayda hem de frekansta lokalize oldukları için idealdir.

JPEG2000 gibi görüntü sıkıştırma teknikleri, görüntüleri daha verimli temsil etmek için waveletlerden yararlanır.

Ayrıca wavelet dönüşümleri, ana görüntü özelliklerinden gürültü bileşenlerini ayırmaya yardımcı olarak etkili bir gürültü azaltımı sağlar.

Kısmi Diferansiyel Denklemler ve Varyasyonel Yöntemler

Daha gelişmiş görüntü işleme görevlerinde, özellikle görüntü restorasyonu ve segmentasyon gibi işlemlerde, kısmi diferansiyel denklemler (PDE’ler) ve varyasyonel yöntemler devreye girer. Bu teknikler, bir enerji fonksiyonu oluşturup, bu enerjiyi minimize eden görüntüyü bulmayı içerir; bu problem, varyasyonlar hesabı ve PDE’lere derinlemesine bağlıdır.

Örneğin Perona-Malik Difüzyon denklemi gibi yöntemler, kenarları koruyarak görüntüyü yumuşatır; bu da önemli özelliklerin korunması için kritiktir.

Bu, gürültüyü azaltırken keskin kenarları koruyan, orijinal görüntüye sadakati yumuşaklıkla dengeleyen Toplam Varyasyon (TV) Minimizasyonu optimizasyon tabanlı bir yaklaşımdır.

Ters Problemler

Bulanıklık giderme, eksik kısımların doldurulması (inpainting) ve süper çözünürlük gibi birçok görüntü işleme sorunu ters problemler olarak adlandırılır. Bu durumlarda, bozulmuş gözlemlerden orijinal görüntüyü geri kazanmayı amaçlarız. Bu geri kazanım süreci genellikle şu şekilde edilir:

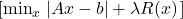
Burada:

• ( A_x_ -b ) bozulmayı (örneğin, bulanıklığı) modellemektedir.
• ( R(x) ), yumuşaklık veya seyrek yapı gibi ön bilgileri içeren bir düzenlileştirme terimidir.
• Lambda değeri ise, gözlemlenen veriye bağlılık ile düzenlileştirme terimi arasında denge kuran bir parametredir.

Gradyan inişi ve daha gelişmiş algoritmalar gibi optimizasyon teorisi teknikleri, bu problemlerin çözümünde hayati öneme sahiptir.

Bu matematiksel temelleri anlamak, dijital görüntülerin nasıl çalıştığına dair takdirimizi derinleştirmenin yanı sıra, yeni teknikler geliştirmemiz için de kullanılır. İster öğrenci, ister araştırmacı ya da meraklı olun; görüntü işlemenin matematiğine yapılan bu yolculuk sonraki adımlarımızda bize ışık tutacak…

Yani bir sonraki yazımızda görüşmek üzere… değil tabiki. Bu sefer normalden uzun yazarak OpenCV’nin kullanımına da gireceğim. Öyleyse devam edelim.

OpenCV ile Dijital Görüntü İşleme

Az buçuk matematiğini kavradığımıza göre konunun, şimdi sol baştan saymaya başlayalım. Neyi? OpenCV’nin sağladığı güzide özellikleri.

Başta temel görüntü işleme şeysileri ile başlayalım.

OpenCV’yi import edelim.

Görüntüler ile çalışacaksak bilmemiz gereken 3 şey var. İlki bir görüntü dosyası nasıl okunur. Efendim bu iş için biz imread fonksiyonunu kullanıyoruz.

İkinci ve en önemli konu, okuduğumuz görüntü Python için ne anlam ifade ediyor. Bunu Spyder Editörden aldığım bir ekran görüntüsü ile ifade edeceğim.

lenna.png 512x512 boyutunda 8 bit bir görüntü olduğu için OpenCV bunu 512x512x3 lük bir matrix haline getiryor.

Ve en önemlisi, birazdan bu dosya üzerinde işlemler uyguladıktan sonra değişimleri kaydetmek isteyeceğiz. İşte bu işi de imwrite ile yapıyoruz

Bu kadarını anladıysak hadi şimdi bir sonraki adımlara geçelim.

---

Bu noktada Lenna bacımızı anmadan da geçmeyelim.

Dünya ahret bacımız olan bu hanımefendi, bilgisayar ve görüntü işleme dünyasında oldukça tanınan bir figürdür.

Lenna’nın hikayesi bir abazalık içeren güzel bir hikayedir. Bu aşina olduğumuz fotoğrafı, 1973 yılında Playboy dergisinin bir sayısında yayınlanmıştı. Aynı yıllarda, ABD’deki University of Southern California (USC)’nin Görüntü İşleme Araştırma Laboratuvarı’nda (SIPI) araştırmacılar, yeni bir görüntü işleme algoritması üzerinde çalışıyordu. Görüntü işlemeyi test etmek için yüksek kaliteli bir dijital görüntüye ihtiyaçları vardı. Ancak o dönemde dijital görüntüler nadirdi. Araştırmacılar, laboratuvarda (?) tesadüfen (!!!!) buldukları Playboy dergisini tarayarak Lenna’nın fotoğrafının üst kısmını, omuzlarının üstünden, yüzünün yer aldığı bölgeyi, görüntü işlemek için aldı (aklımda peki alt kısmı diye bir soru hep beliriyor, neyse…).

Görüntü, bilgisayar ekranında yüksek çözünürlükle görünebilen, dönemin şartlarına göre oldukça iyi bir test görüntüsü olarak kullanılmaya başlandı. Lenna’nın yüzünün görüntüsü, kısa sürede akademik yayınlarda ve konferanslarda standart bir test görüntüsü haline geldi. Özellikle görüntü işleme algoritmalarını test etmek ve karşılaştırmak için kullanılan bir referans oldu. Görüntünün renk detay ve piksel derinliği açısından zengin olması, insan yüzü gibi tanınabilir bir nesnenin bulunması döneminde görüntü işleme topluluğunda bir standart haline gelmesini sağladı.

Ancak popülerleşmesi o kadar iyi bir şey de olmadı. Çoğu insan için cinsiyetçi olarak bulunan bu görüntü, Playboy dergisinin bir telif çatışmasına dönüştü ancak, Lenna’yı Lenna yapan şey tam bu anda oldu. Kendisinin yüzünün görüntüsünün bilimsel amaçlarla kullanılmasından etkilendiğini düşündüğümüz bu güzel kalpli hanımefendi, görüntü işleme için görüntüsünün 512x512’lik olan bu kısmının telifsiz olarak kullanılmasına izin vererek bugün OpenCV dediğimiz zaman kendisini her yazıda görebilmemize vesile kıldı.

Neyse şimdi OpenCV ile neler yapabileceğimize girelim…

Boyutlandırma ve Ölçeklendirme

Yeniden boyutlandırma veya görüntü ölçekleme, bir görüntünün boyutunu değiştirme sürecini ifade eder. Bu, görüntüdeki piksel sayısını artırarak veya azaltarak yapılabilir, bu da görüntünün fiziksel boyutlarını (örneğin genişlik ve yükseklik) değiştirir. Bir görüntü yeniden boyutlandırıldığında, yeni piksellerin eklenmesi veya mevcut piksellerin kaldırılması gerekir. Bu yeni pikselleri doldurmak için kullanılan algoritmaya enterpolasyon yöntemi denir ve farklı enterpolasyon yöntemleri farklı görüntü kalitesi seviyelerine neden olur. Bir görseli yeniden boyutlandırma, genellikle bir görseli belirli bir amaç için küçültmek veya büyütmek, örneğin bir web sitesinin belirli bir boyutuna sığdırmak veya belirli bir boyutta basmak için kullanılır. Şimdi lena bacımız üzerinde bunları deneyelim. Normalde lenna bacımız 512x512 boyutunda ama hadi biz bunu 320x400 yapalım.

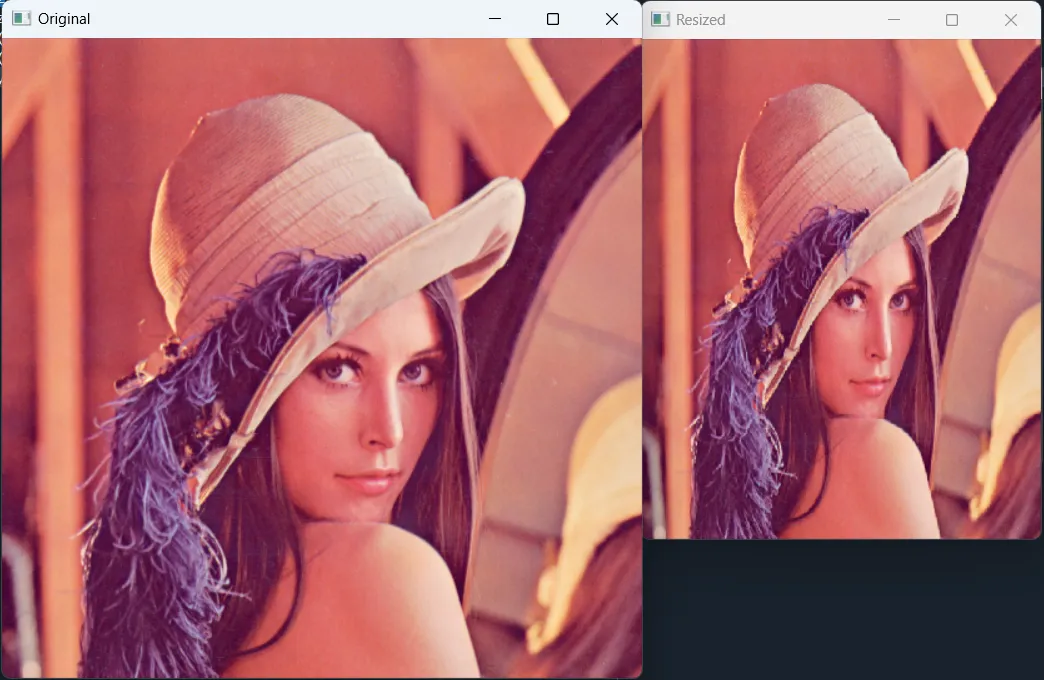
OpenCV’de, aşağıdakiler de dahil olmak üzere envai yeniden boyutlandırma yöntemleri mevcuttur:

• cv2.INTER_NEAREST: Bu, en basit ve en hızlı enterpolasyon yöntemidir. Yalnızca yeni görüntü boyutuna en yakın pikseli seçerek “bloklu” veya “pikselli” bir görüntü elde edilmesini sağlar.
• cv2.INTER_LINEAR: Bu yöntem doğrusal enterpolasyon algoritması kullanır. En yakın komşu yönteminden daha pürüzsüz bir görüntü sağlar, ancak bazı ayrıntı kayıplarına neden olabilir.
• cv2.INTER_AREA: Bu yöntem, alan tabanlı bir enterpolasyon algoritması kullanır. Özellikle görüntüleri küçültmek için kullanışlıdır ve bu amaç için doğrusal enterpolasyon yönteminden daha iyi sonuçlar üretebilir.
• cv2.INTER_CUBIC: Bu yöntem, kübik enterpolasyon algoritması kullanır. Genellikle görüntüleri büyütmek için kullanılır ve yüksek kaliteli sonuçlar üretebilir, ancak hesaplama açısından da pahalıdır.
• cv2.INTER_LANCZOS4: Bu yöntem bir Lanczos enterpolasyon algoritması kullanır. Özellikle ince ayrıntılara ve dokulara sahip görüntüler için yüksek kaliteli sonuçlar üretir, ancak hesaplama açısından pahalıdır.

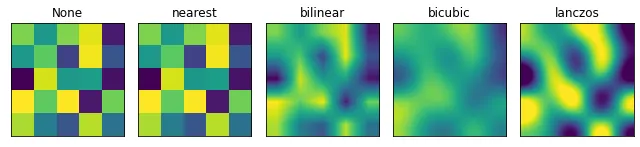
Bunlar en sık kullanılan enterpolasyon yöntemidir, aklınızda bulunsun, yeniden boyutlandırma işlemi ile görüntüye ve ulaşmak istediğiniz hedefe bağlı olarak uygun yöntemi kullanabilirsiniz.

Görüntüyü Evirme, Çevirme

OpenCV’de bir görüntüyü döndürmek, kırpmak ve çevirmek için aşağıdaki yöntemleri kullanabilirsiniz:

Kırpma:

Satırların ve sütunların başlangıç ve bitiş konumlarını belirleyerek bir görüntüyü kırpmak için numpy indekslemeyi kullanabilirsiniz.

Döndürme:

Çevirme ve döndürme işlemleri işlem için bir matris gerektirir. Döndürme matrisi oluşturmak için cv2.getRotationMatrix2D()işlevini kullanabilir ve ardından döndürmeyi görüntüye uygulamak için cv2.warpAffine() işlevini kullanabilirsiniz. cv2.getRotationMatrix2D() işlevi, giriş olarak dönüş merkezini, dönüş açısını (derece cinsinden) ve bir ölçeklendirme faktörünü alır.

Çevirmek:

Bir görüntüyü çevirmek demek onu x ve y eksenleri boyunca belirli sayıda piksel kaydırmak anlamına gelir. Görüntünün kaydırılması gereken piksellere göre hesap yapılır. Ardından bir çeviri matrisi (M) tanımlanır.

Bir çeviri matrisi oluşturmak için cv2.getRotationMatrix2D()işlevini kullanabilir ve ardından çeviriyi görüntüye uygulamak için cv2.warpAffine() işlevini kullanabilirsiniz. Çeviri matrisi, matriste x ve y ofset değerleri belirtilerek oluşturulur

Görüntü Rengi ve Piksel Renk Manüplasyonu

OpenCV kullanarak bir görüntünün renk bitlerini elde etmek için, okuduğumuz dosyadan oluşturduğumuz görüntü matrisinin öğelerinin veri türünü kontrol etmek için dtype özniteliğini kullanabilirsiniz. Veri türü, her bir renk kanalı için kullanılan bit sayısını gösterecektir (örneğin, lenna bacımızın renk derinliği için 8 bit).

Çıktı olarak bize şunu verecektir:

uint8

Şimdi gel gelelim bu 8 bitlik görüntüyü kanallarına ayırmaya. Renk kanalları nedir sorusu ile başlayalım. Renk kanalı, renkli bir görüntünün veya videonun belirli bir yönünü ifade eder. Dijital görüntülerde, renk kanalları tipik olarak 2 boyutlu bir piksel dizisi olarak temsil edilir; burada her piksel, görüntüdeki belirli bir konumdaki renk kanalının yoğunluğuna karşılık gelen belirli bir değerle (örn. 0–255) temsil edilir.

Dijital görüntülerdeki en yaygın renk kanalları Kırmızı, Yeşil ve Mavi’dir (RGB). Bu kanallar, renkleri farklı şekillerde birleştirerek tam renkli bir görüntü oluşturmak için kullanılır. Görüntüdeki her pikselin üç kanalın her biri için bir değeri vardır ve bu değerler birleştirilerek o pikselin son rengi belirlenir.

Örneğin, 8 bitlik bir RGB görüntüsünde, her kanal (kırmızı, yeşil ve mavi) 8 bit ile temsil edilir ve 256 farklı yoğunluk düzeyine izin verir. Kırmızı, Yeşil ve Mavi kanallarında sırasıyla değerlere (255, 0, 0) sahip bir piksel, nihai görüntüde saf kırmızı olarak görünür.

HSV (Ton, Doygunluk, Değer), HSL (Ton, Doygunluk, Açıklık) gibi diğer renk uzayları da bir görüntüdeki renkleri temsil etmek için farklı renk kanalları kullanır ama şimdilik onlara girmeyeceğiz.

OpenCV’de cv2.split() işlevini kullanarak bir görüntüyü kendi renk kanallarına ayırabilirsiniz. İşlev, bir görüntüyü (bir numpy dizisi biçiminde) girdi olarak alır ve her bir renk kanalı için bir tane (renkli bir görüntü için Mavi, Yeşil, Kırmızı sırasına göre) bir dizi numpy dizisi döndürür. Şimdi her bir kanalı ayırarak görelim.

Akıllardaki soru şu an şu: neden cv2.merge diye bir şey kullandık. Çünkü kanalları tek başına çizdirmek istersek şöyle bir çıktı elde edeceğiz.

Çünkü her bir kanal aslında 2 bitlik bir imaj da sayılabilir. Bu yüzden biz her bir kanalı yukarıda anlattığım gibi kendi kısmına merge ederek gösterdik.

Şimdi artık bir başka önemli konuya değinebiliriz.

Morfolojik İşlemler

Morfolojik işleme, görüntüleri işlemek için basit şekiller (yapılandırma öğeleri olarak adlandırılır) kullanan bir görüntü işleme tekniğidir. Bu basit şekiller, bir görüntüdeki nesnelerin şeklini, boyutunu ve yönünü işlemek ve analiz etmek için kullanılır. Görüntü üzerinde hareket ettirilen küçük bir çekirdek (kernel veya structuring element) matris ile matris çarpımı yapılarak gerçekleştirilir (daha birkaç metre yukarıda bir yerde yazmıştım). En temel morfolojik işlemler dilatasyon ve aşındırmadır.

OpenCV’de, cv2.morphologyEx() işlevi kullanılarak morfolojik işlemler gerçekleştirilebilir. Bu işlev üç parametre alır: giriş görüntüsü, morfolojik işlem (erozyon veya genişleme gibi) ve işlem için kullanılan yapılandırma matrisi (veya çekirdek).

Morfolojik yöntemler ile başlayalım.

Öncelikle 5x5 boyutunda bir kernel tanımlayalım.

İlk olarak genişletme (dilation), görüntüdeki bir nesnenin sınırlarına pikseller ekleyerek nesnenin daha büyük görünmesini sağlar. Aşındırma (erosion) ise, pikselleri bir nesnenin sınırlarından kaldırarak daha küçük görünmesini sağlar. Bu işlemler genellikle nesnelerin siyah bir arka plan üzerinde beyaz pikseller olarak temsil edildiği ikili görüntülere uygulanır.

Diğer bir morfolojik işlem olarak aşındırma (erosion) yer alır. İşlem, görüntüdeki küçük parazitleri gidermek veya bir nesnedeki küçük delikleri doldurmak için kullanılır. Nesnelerin kenarlarından piksel kaybına neden olarak, nesneleri küçültür ve ince detayları ortadan kaldırır.

Diğer morfolojik işlemler bu iki işlemi esas alarak yapılır. Örneğin açma (opening) işlemi aşındırma işlemi sonrasında genişletme uygulanmasıdır. Küçük gürültü ve nesneleri ortadan kaldırırken, nesnelerin genel şeklini korumaya yardımcı olur. Tam tersine kapama (closing) işlemi ise genişletme sonrası aşındırma uygulanmasıdır. Küçük delikleri doldurur ve nesneleri daha bütünlüklü hale getirir.

Morfolojik Gradyan ise dilation ve erosion arasındaki fark alınarak, nesnelerin kenarlarını vurgulayan bir görüntü elde edilir.

Filtreleme ve Gürültü Giderme

Görüntü işleme uygulamalarında, elde edilen veriler çoğu zaman gürültü içerir. Gürültüyü azaltmak, analiz veya sonraki işlemler için daha temiz veriye ulaşmayı sağlar.

Filtreleme yöntemleri için farklı matematiksel modeller mevcuttur. En sık kullanılanı olan Gaussian blur, görüntüyü yumuşatarak rastgele gürültüyü azaltmada etkilidir.

Kernel boyutu ( (5,5) ) ve sigma değeri ( 0 ), bulanıklığın yoğunluğunu belirler.

Özellikle tuz-biber (salt and pepper) gürültüsü dediğimiz nokta nokta olan gürültülere karşı median blur kullanılır.

Median blur, her pikseli komşu piksellerin medyanı ile değiştirir; bu sayede ani uç değerler ortadan kaldırılır.

Bilateral filtering ise matematiksel olarak en kompleks metod olup, kendisi görüntüde nesne kenarları gibi ani renk dönüşümlerini koruyarak gürültüyü azaltır.

Bu yöntem, hem uzamsal yakınlık hem de piksel benzerliğini göz önünde bulundurarak çalışır.

Kenar Algılama

Görüntüdeki nesne sınırlarını belirlemek, özellikle segmentasyon ve nesne tanıma gibi birçok uygulamada önemlidir. Kenar algılamada kullanılan bazı yöntemlere değineyim.

İlk olarak Sobel methodunu anlatayım. Sobel operatörü, görüntüdeki yatay ve dikey kenarları tespit eder.

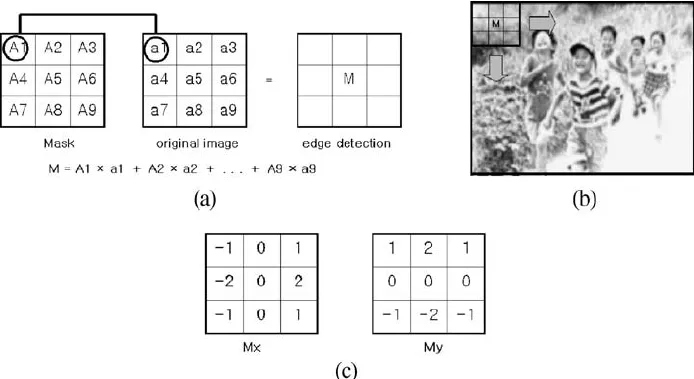
Diyelim ki, I(x,y), görüntünün parlaklık değerlerini temsil ediyor. Sobel operatörü, x (yatay) ve y (dikey) yönlerindeki türevleri yaklaşık olarak hesaplar. Bu yaklaşık hesaplamayı elde etmek için iki ayrı çekirdek kullanılır.

x yönündeki türev için kullanılan Sobel çekirdeği genellikle şu şekilde tanımlanır:

Bu çekirdek, görüntü üzerinde kayan bir pencere ile konvolüsyon yapıldığında, yatay yöndeki yoğunluk değişimini ölçer. Yani, bir pikselin sağındaki ve solundaki değerler arasındaki farkları ağırlıklı olarak hesaplar.

y yönündeki türev için ise şu şekilde tanımlanır:

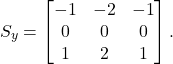
Bu çekirdek ise görüntüde dikey yönde (üst-alt) farkları hesaplayarak, dikey kenarların belirlenmesine yardımcı olur.

Sonuçta her iki çekirdek de, görüntüye konvolüsyon operatörü olarak uygulanır ve kenarın “gücü” ya da magnitüdü (gradients magnitude) hesaplanarak Sobel dönüşümü yapılmış olur.

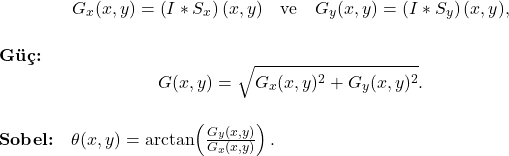
Şimdi bunun OpenCV kodunu yazalım, gerçekten çok (?) uzun:

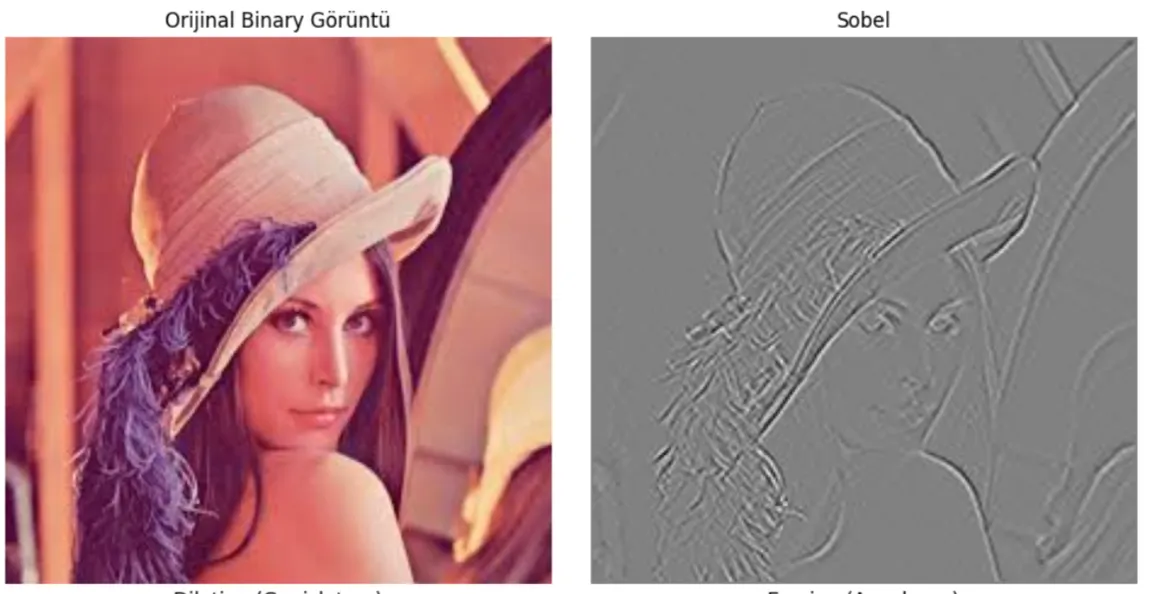
İşte bu gibi uzun fonksiyonların OpenCV içerisinde yer alması bizim için OpenCV’yi değerli yapıyor.

Bir diğer yöntem olarak Canny algoritması, öncelikle gürültü azaltımı (örneğin Gaussian blur) uygular, ardından kenar tespiti yapar.

Histogram İşlemleri

Histogramlar, bir görüntünün parlaklık dağılımını gösterdiğinden, görüntünün kontrastını analiz etmek için kullanılır. Histogram eşitleme (histogram equalization) tekniği, histogramın yeniden dağıtılarak daha dengeli bir parlaklık dağılımı elde edilmesini sağlar; bu sayede görüntüdeki detaylar daha belirgin hale gelir.

Öncelikle histogram hesaplamasını görelim. Histogram hesaplaması bir rengin bir tonu için sahip olduğu değerlerin dağılımlarını verir. Biz bu örnek için kontrast yani Gray Scale için histogram ölçeceğiz.

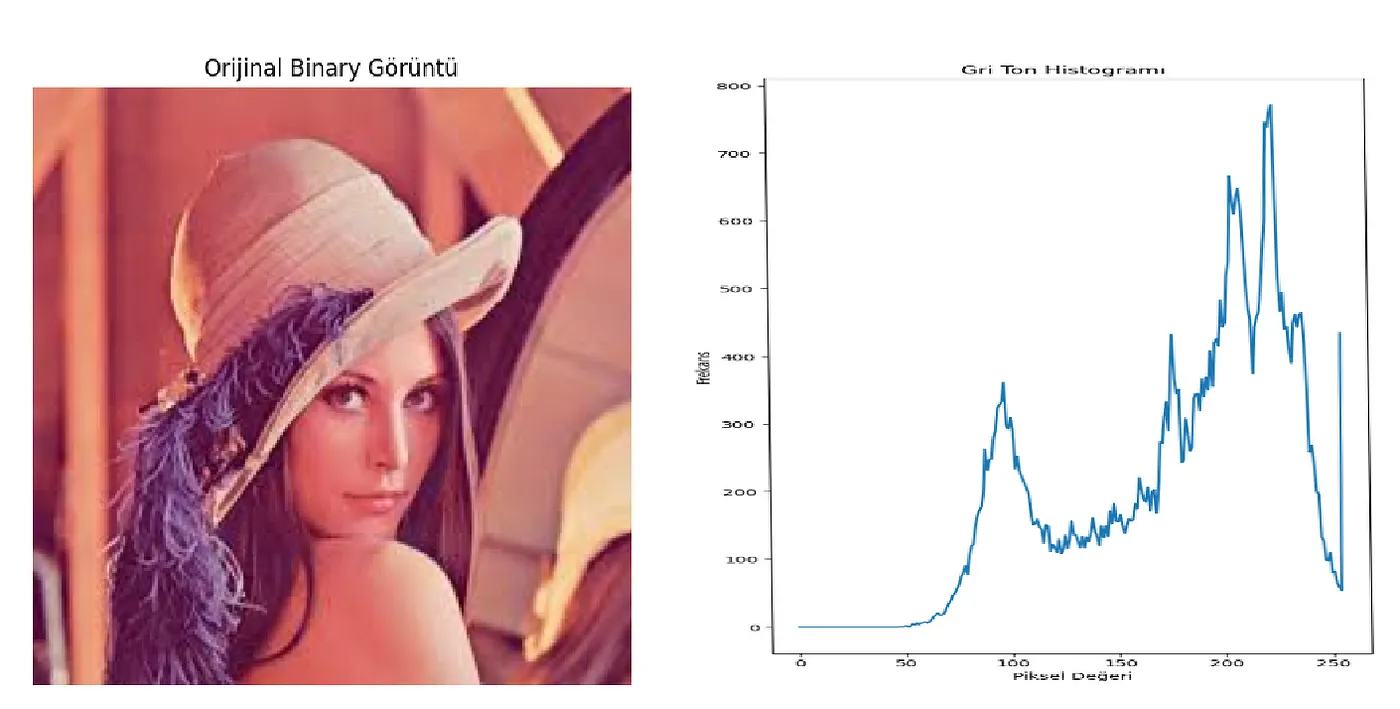
Histogram sonucu gördüğünüz gibi, değerlerin çoğunluğu 50 üstünde olup geneli 200’ler bandında toplanmış durumda.Ancak iyi bir görüntü, görüntünün tüm bölgelerinden piksellere sahip olacaktır ve bu iş için histogram eşitlemesi kullanırız.

OpenCV’de histogram eşitlemesi yapmak için çeşitli işlevlere sahiptir, equalizeHist ile yapılan histogram eşitleme, görüntünün genel kontrastını dikkate alır; CLAHE metodu yani uyarlanabilir histogram eşitlemesinde ise, görüntü “fayans” adı verilen küçük bloklara bölünür (OpenCV’de varsayılan olarak fayans boyutu 8x8’dir). Daha sonra bu blokların her biri önceki gibi histogram eşitlenir.

Gelişmiş Geometrik Dönüşümler

Görüntüyü yeniden boyutlandırma, döndürme ve çevirmeye ek olarak, daha ileri seviye dönüşümler de mevcuttur.

Affine Dönüşümler

Affine dönüşümler, görüntüde ölçekleme, döndürme, çevirme ve eğme (shear) gibi işlemleri aynı anda yapabilir.

Buna ek olarak perspektif dönüşüm (homography), bir görüntüyü farklı bir bakış açısına uyarlamak için kullanılır.

Gerçekten Bitirirken

Perspektif dönüşümleri de anlatarak OpenCV konusunda bayaa bir örnek vermiş ve matematiğini de paylaşmış oldum. Dijital görüntü işleme dünyasının temel taşlarından başlayıp, OpenCV kullanmaya girişe hatta OpenCV’nin ileri seviye tekniklerine kadar geniş bir yelpazede kod örnekleri ile bu konuyu el aldım.

Filtreleme, kenar algılama, histogram işlemleri, gelişmiş dönüşümler, özellik tespiti, görüntü birleştirme gibi konular, modern görüntü işleme uygulamalarında sıkça kullanılan araçlardır ve umarım gerek teknik örnekleri gerek matematiksel ifadeleri ile görüntü işlemeyi anlamak isteyen sizler için güzel bir yazı yazmış olurum ve umuyorum zevkle okuyup buraya kadar gelmişsinizdir.

O zaman, Lenna yoldaşınız olsun.

Bir sonraki yazıda görüşmek üzere. Esen kalın…